深入理解透视矩阵

图形学渲染是将虚拟的三维世界转换成二维像素图片，在这个转换过程中，坐标变换不可或缺，其中透视投影是实现近大远小等透视效果的数学原理。由于左右手系、深度范围等多种影响因素，导致透视投影本身就有多个变种矩阵。本文试图寻找一种矩阵推导流程，明确各种影响因素的影响范围和具体表现。（本文采用列矩阵，因而矩阵变换为左乘）

GAMES101 的推导方式

闫令琪老师在 GAMES101 课程中给出了一种通俗易懂的透视矩阵推导方式，这里罗列其思考过程：

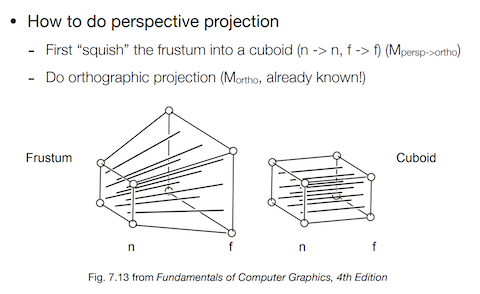
p2o.png

透视投影过程分为三步：

  1. 将平截头体挤压成一个长方体（压缩远平面，挤压过程为一个齐次矩阵 MatP2O）
  2. 对长方体做一个正交投影（正交投影则仅是一个普通的缩放平移矩阵，正交投影也是一个齐次矩阵 MatOrtho）
  3. 最后可算出透视矩阵：MatPersp = MatOrtho * MatP2O（列矩阵，先进行 P2O，后进行 Ortho）

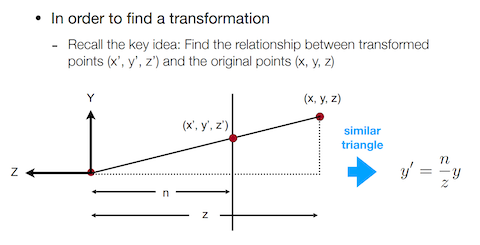
similar_triangle.png

根据相似三角形原理，挤压远平面之后的 x 和 y 都与 z 值成比例关系，上图中的 n 和 z 均为带符号的坐标值，并非距离。

homogeneous.png

在齐次坐标中，只要齐次分量非 0，同一个 3D 坐标可以有无数个齐次坐标，闫老师这里选择了 z 作为齐次分量。

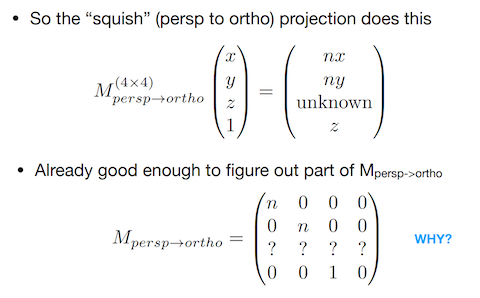
matp2o.png

根据压缩前后的坐标关系，构造 MatP2O 矩阵，仅欠缺矩阵的第三行。

near_plane.png

压缩过程我们希望近平面和远平面的 z 坐标保持不变，上图中的 n 也是带符号的坐标值，并非距离。

far_plane.png

根据近远平面 z 坐标不变的条件我们可以得到二元一次方程组，其中 n 和 f 也是带符号的坐标值，不是距离。

perp.png

算出第三行，我们得到了挤压矩阵为：

其中，n 和 f 为带符号的坐标值。挤压矩阵不改变左右手性。

有了压缩矩阵，我们还需要一个正交投影矩阵。

普通的正交投影仅是缩放和平移，不改变左右手性。给定 l 和 r 为左右边界，b 和 t 为下上边界，n 和 f 为前后边界，投影后为: 也就是映射关系为：（这里 l、r、b、t、n、f 都是带符号的坐标值，非距离）

那么投影前后的坐标关系为：

对应投影矩阵为：

由于 n 映射为-1，f 映射为 1，那么当 n < f 时，该投影矩阵不改变左右手性，当 n > f 时，该矩阵会改变左右手性

以上，我们得到第一个透视投影矩阵：

其中，n 和 f 为带符号的坐标值，非距离。

既然纯手工推导出一个透视矩阵，我们当然要验证一下其正确性，就跟 OpenGL 数学库 glm 对比一下。

与 glm 透视矩阵对比

glm 中透视矩阵默认是右手坐标系，深度映射范围是 [-1, 1]，需要四个参数：

对应透视矩阵的代码为：

glm::mat4 MatPerspTest1 = glm::perspective(glm::radians(45.0f), 1920.0f/1080.0f, 0.1f, 50.0f);

打印出其值：

同样的参数应用到 MatPersp1，则有：

带入数值，可得透视矩阵为：

对比 MatPerspTest1 和 MatPerspTest2，我们发现，抛开浮点精度的差异之外，两者相差一个负号，why？

接下来，让我们看看书本怎么说。

《3D 游戏与计算机图形学中的数学方法》中的推导

《Mathematics for 3D Game Programming and Computer Graphics Third Edition》一书中 5.5.1 章节，使用数学方法推导出标准透视矩阵，这里就不照搬推导过程，结论如下图：

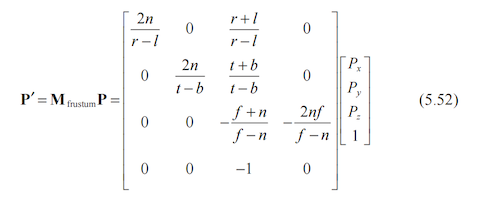
math_persp.png

需要注意的是，书中基于右手坐标系，并且 Z 值映射到 [-1, 1]，区别在于，书中推导过程使用了 -z 作为透视矩阵的齐次分量，并且，上图中，r、l、t、b 四个是带符号的坐标值，而 n 和 f 为距离。

为了避免混淆，这里将表示距离的 n 和 f 替换成 zNear 和 zFar，我们得到第二个透视矩阵：（我们的推导中，n 和 f 带符号，zNear 和 zFar 是距离）

如果将 n=-zNear，f=-zFar 带入我们推导的 MatPersp1，我们就会发现，MatPersp1 和 MatPersp2 仅存在两点不同：

  1. 第一二行的第三个值不同
  2. 整体相差一个负号

针对第一个问题，一般情况下 r=-l，t=-b，那么第一二行的第三个值都会是 0。针对第二个问题，相差一个负号的原因在于推导透视矩阵的过程我们使用了 z 作为齐次分量，而书中使用了 -z。

由此我们可以看出，只要将我们的透视矩阵乘以一个 -1，就能得到书本中的标准 OpenGL 右手系透视矩阵。另外，将我们的透视矩阵乘以任意非零 scale，得到的矩阵也具备透视矩阵功能，只不过齐次分量成了 z*scale，scale不为0。

通过查看 glm 源码，我们发现，其中的 perspectiveRH_NO 函数所实现的右手系透视矩阵就是 -MatPersp1。

书本中还推导了当 zFar 趋于无穷远时的透视矩阵，也就是在原有基础上求极限。

另一种矩阵形式

前面在计算 MatPerspTest2 矩阵给出了如下等式：

可以算出：

同样的：

我们得到第三个透视矩阵：

透视矩阵思考点

整理一下思路，我们推导透视矩阵的过程中，需要处理的问题在于：

  1. 左右手性？（正负半轴？）
  2. 齐次坐标的 w 分量？（齐次分量应该存放什么值？）
  3. 深度映射范围？（ReversedZ？）

其中，1 和 2 在于推导挤压矩阵的过程需要考虑，3 则在于推导后续正交矩阵需要考虑。

对于右手坐标系：

  1. 世界坐标使用右手系，相机看向 Z 负半轴，也就是 n=-zNear，f=-zFar
  2. 齐次分量存放 -z
  3. 针对 OpenGL，深度映射范围是 n=>-1，f=>1，由于 n > f，此映射导致变换了手性（右手系变左手系，不过由于投影和透视除法之后拆分为屏幕坐标和深度值，也就没那么在意手性）

对于左手坐标系：

  1. 世界坐标使用左手系，相机看向 Z 正半轴，也就是 n=zNear, f=zFar
  2. 齐次分量存放 z
  3. 针对 Direct3D，深度映射范围是 n=>0，f=>1，由于 n < f，此映射不改变手性

值得一提的另外一点是关于实践中 aspect 的取值。我们知道 aspect 是宽高比，那么具体一点是什么东西的宽高比？以下我们列出来可选的几种宽高度量方式：（参考 https://zhuanlan.zhihu.com/p/113662566）

  1. 屏幕坐标范围的宽高（通过 glfwGetWindowSize 获得，就是鼠标坐标的范围，此宽高与像素分辨率并没有绝对的映射关系，一般是 1:1）
  2. 渲染 FrameBuffer 的像素阵列宽高（通过 glfwGetFramebufferSize 获得）
  3. 显示器物理大小的宽高，单位毫米（通过 glfwGetMonitorPhysicalSize 获得）

透视矩阵参与的渲染过程中，得到的内容是先放到 FrameBuffer 的像素中，而后被显示在显示器屏幕上。我们的目标是人眼看到的物体宽高比刚好是数值上的宽高比，因此，应该用 FrameBuffer 像素数量的 widget 和 height 所对应的实际物理长度(mm)来计算宽高值。

FrameBuffer 只能计算像素数量的比值（FrameBufferPixelCountAspect，简称 FBPCAspect），单个像素是没有大小的（可以看成正方形）。但是在显示器上，单个像素是有大小的，也就是存在单个像素宽高比（MonitorPixelAspect，简称 MPAspect），那么，为了在显示器上看到宽高比正常的内容，传递给透视矩阵的宽高比应该是 aspect = FBPCAspect * MPAspect（没错，不同显示器要用不同的 aspect。如果两个显示器的 MPAspect 不同，那么，同一张的图片放到这两个显示器上看会出现宽高比不一致）

如果 MPAspect 不等于 1，按照 FrameBuffer 每个像素都是正方形的逻辑来看，存粹 FrameBuffer 中的渲染结果会被拉伸或压缩，但是，显示到屏幕上的时候，会由于屏幕像素存在同样的比例而显示效果正常。

最后，在做多个 pass 的渲染时，RenderTexture 的内容被重新采样和渲染，只要保证渲染后的像素宽高比跟原 FrameBuffer 的像素宽高比一致就好。

完整运算流程

基于前面对透视矩阵的推导和分析，现给出如下完整推导所有类型透视矩阵的流程：（这里仅考虑 l=-r，b=-t 的情况）

  1. 根据目标左右手性确定 n 和 f 的值（左手系为正数、右手系为负数）
  2. 将 n 和 f 的值代入 MatP2O 得到压缩矩阵
  3. 如果是右手系，handedness = -1；如果是左手系，handedness = 1（保证齐次分量永远是 z 的绝对值）
  4. 根据目标深度映射范围算出正交投影矩阵 MatOrtho（这一步可能会改变原有的左右手性）
  5. 透视矩阵为：MatPerspective = MatOrtho * handedness * MatP2O

UE 透视矩阵

应用上述完整运算流程，我们来推导一下 UnrealEngine 中的透视矩阵：

FORCEINLINE FPerspectiveMatrix::FPerspectiveMatrix(float HalfFOV, float Width, float Height, float MinZ, float MaxZ)
  : FMatrix(
    FPlane(1.0f / FMath::Tan(HalfFOV), 0.0f,                                 0.0f,                                                                   0.0f),
    FPlane(0.0f,                       Width / FMath::Tan(HalfFOV) / Height, 0.0f,                                                                   0.0f),
    FPlane(0.0f,                       0.0f,                                 ((MinZ == MaxZ) ? (1.0f - Z_PRECISION) : MaxZ / (MaxZ - MinZ)),         1.0f),
    FPlane(0.0f,                       0.0f,                                 -MinZ * ((MinZ == MaxZ) ? (1.0f - Z_PRECISION) : MaxZ / (MaxZ - MinZ)), 0.0f)
  )
{ }

上述代码来自 UnrealEngine 中的 PerspectiveMatrix.h 文件。

根据流程，有：

  1. UE 的世界坐标是左手系，透视矩阵采用左手系，n=zNear，f=zFar
  2. 压缩矩阵为：
  3. 左手坐标系，handedness = 1
  4. UE 使用的深度映射范围是 n=>0，f=>1（FReversedZPerspectiveMatrix 实现的版本则是反过来的），我们得到正交矩阵：
  5. 透视矩阵为：
  6. 我们换一种形式： 带入上式，则：

将 MatPerspective2 与 UE 的实现做对比，可以发现：

  1. 在 MinZ 不等于 MaxZ 的情况下完全一致
  2. UE 源码中的 HalfFOV 是 fovx/2
  3. 在 MinZ 等于 MaxZ 的情况其实就是 zFar 趋于正无穷的极限情况，有兴趣的读者可以自行求极限

总结

一般来说，透视矩阵具备如下形式：（列向量构成的矩阵）

我们可以简单判断其推导条件：

  1. e 为 1 则表示该矩阵在左手系下推导得到，看向 Z 正半轴；e 为-1 则为右手系，看向 Z 负半轴
  2. c 的分子为 zNear+zFar 表示深度映射范围是 [-1, 1]
  3. c 的分子为 zFar 表示深度映射范围是 [0, 1] 并且 zFar=>1
  4. c 的分子为 zNear 表示深度映射范围是 [0, 1] 并且 zNear=>1，也就是 ReversedZ
  5. c 是常数则表示该矩阵是 zFar 趋于正无穷的情况